Please links to the original and only refer to this as a mirror.
Forth is an unusual computer language that has probably been applied to more varied projects than any other. It is the obvious choice when the project is exceptionally demanding in terms of completion schedule, speed of execution, compactness of code, or any combination of the above.
It has also been called “…one of the best-kept secrets in the computing world.” This is no exaggeration: large corporations have purchased professional Forth development systems from vendors such as Laboratory Microsystems, Inc., Forth, Inc. or MicroProcessor Engineering, Ltd. and sworn them to secrecy.
Some speculate (unkindly) that corporate giants prefer to hide their shame at using Forth; but I believe they are actually concealing a secret weapon from their rivals. Whenever Forth has competed directly with a more conventional language like C it has won hands down, producing smaller, faster, more reliable code in far less time. I have searched for examples with the opposite outcome but have been unable to find a single instance.
We will use Win32Forth for these illustrations. Download the file
w32for42.exe
and double-click on it to install on any Windows 95, 98, NT, ME, or XP –equipped machine.
The compressed files will then decompress themselves. They should also install a program group on your desktop.
Now start Win32Forth by opening the program group and clicking on the appropriate icon.
It should respond by opening a window and writing something like
32bit Forth for Windows 95, and NT
Compiled: July 23rd, 1997, 5:11pm
Version: 3.5 Build: 0008 Release Build
Platform: Windows 95 Version: 4.0 Build: 16384
491k bytes free
2,719 Words in Application dictionary
1,466 Words in System dictionary
4,185 Words total in dictionaries
8,293 Windows Constants available
Loading Win32For.CFG
*** DON'T PANIC, Press: F1 NOW! ***
You can use UPPER or lower-case to type commands and data. Win32Forth is case-insensitive.
You can also start the WinView editor by clicking on its icon in the program group. The features of the editor are fairly standard and self-explanatory. Make sure to set the preferences (Ctl-Shift-P or use the Edit drop-down menu) to your own liking. Among other things, WinView is written in Forth (the complete source is included) and is integrated with Win32Forth so that compiling errors pop up in the editor.
In the Win32Forth window, now type
BYE <cr>
The Win32Forth window immediately closes.
What just happened? Forth is an interactive programming language consisting entirely of subroutines, called words in Forth jargon.
Interactive means you type things in at the keyboard and the machine responds. We will see some details of how it does this below.
A word is executed (interactively) by naming it. We have just seen this happen:
BYE is a Forth subroutine meaning “exit to the operating system”. So when we
typed BYE BYE was executed, and the system returned control to
Windows.
Click on the Win32Forth icon again to restart Forth. Now we will try something a little more complicated. Enter:
2 17 + . <cr> 19 ok
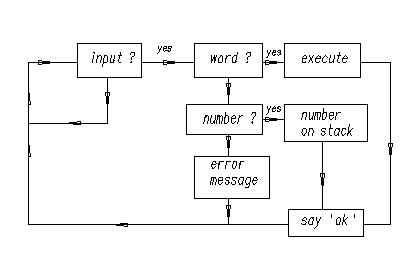
What happened? Forth is interpretive. A small program called the “outer interpreter” continually loops, waiting for input from the keyboard or from a mass storage device. The input is a sequence of text strings (words or numbers) separated from each other by the standard Forth delimiter: one or more ASCII blank (32decimal = 20hex) characters.
The text strings can be interpreted in only three ways: words (subroutine names), numbers, or “not defined”.
The outer interpreter tries first to look for an incoming word in the dictionary (a list of already-defined subroutine names). If it finds that word, the interpreter executes the corresponding code.
If no dictionary entry exists, the interpreter tries to read the input as a number. If the string satisfies the rules defining a number, it is converted to a number in the machine’s internal representation, and stored in a special memory location, called “the top of the stack” (TOS).
In the above example, Forth interpreted 2 and 17 as numbers, and pushed
them both onto the stack.
+ is a pre-defined word as is ., so they were looked up and executed.
+ added 2 to 17 and left 19 on the stack.
The word . (called “dot”) removed 19 from the stack and displayed it on the
standard output device (in this case, CRT).
The diagram below is a flow chart representing the actions performed by the Forth outer interpreter during interpretation.

We might also have said:
HEX 0A 14 * . <cr> C8 ok
(Do you understand this? Hint: DECIMAL means “switch to decimal arithmetic”,
whereas HEX stands for “switch to hexadecimal arithmetic”.)
If the incoming text can neither be located in the dictionary nor interpreted
as a number, Forth issues an error message. Try it: type X <cr> and see
X
Error: X is undefined
or type THING <cr> and see
THING
Error: THING is undefined
Finally, here is the obligatory “Hello, World!” program. Forth lets you output
text using the word ." as follows (we will explain in §4 below what : and
; mean):
: hi ." Hello, World!" ; ok
Now type in hi and see what happens:
hi Hello, World! ok
This can be elaborated with words that tab, emit carriage returns, display in colors, etc. but that would take us too far afield.
(The word ." means “Display the string, following the obligatory blank space
and terminated by the close-quote " on the standard output device.”)
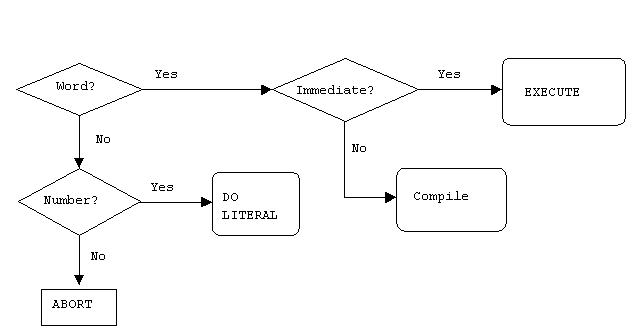
Forth belongs to the class of Threaded Interpretive Languages. This means it can interpret commands (subroutines or programs) typed in at the console, as well as create (compile) new subroutines and programs. The compiler in a traditional language has the structure shown below:

To compile and test a program in a traditional language such as Fortran, C or Pascal, one prepares an input (source) file, submits it to a black box that someone else created (the compiler) and then runs the resulting executable file (which is generally in machine language). This process can be so tedious that most program development in traditional languages must be supported by an elaborate set of programs called the “environment”, consisting of integrated editors, debuggers, version control catalogues and the like.
The outer interpreter/compiler of a Forth system looks like this:

Forth has little in common with the traditional compilation method. Although the Forth interpreter/compiler diagrammed above looks complicated, it is simplicity itself compared with the contents of the oval blob representing a traditional black-box compiler.
A continuous loop waits for input—from the keyboard, a disk file or whatever—and acts on it according to its nature. Input consists of a sequence of words and numbers. If a name is recognized it is executed; if it is not in the dictionary (where else would you keep a list of words?) Forth tries to convert it to a number and push it on the stack. If this is impossible, Forth aborts execution, issues an error message and waits for more input.
As we shall see below, what makes Forth a compiler as well as an interpreter is the set of words (Forth subroutines) that, when they are typed in and executed, create new Forth subroutines.
The compiler is one of Forth’s most endearing features. Unlike most other high-level languages, the Forth compiler is part of the language. (LISP and its dialects also make components of the compilation mechanism available to the programmer.) That is, its components are Forth words available to the programmer, that can be used to solve his problems.
In this section we discuss how the compiler extends the dictionary. As noted above, normally a Forth system awaits input, and interprets (and executes it). We say the system is normally in interpret mode.
Forth uses special words to create new dictionary entries, i.e., new words. The
most important are : (“start a new definition”) and ; (“terminate the
definition”).
Let’s try this out: enter
: *+ * + ; <cr> ok
What happened? The word : was executed because it was already in the
dictionary. The action of : is:
*+ and switch from interpret to
compile mode.*+ is thus to execute sequentially the previously-defined
words * and +.; is special: when it was defined a bit was turned on in its
dictionary entry to mark it as IMMEDIATE. Thus, rather than writing down
the address of ;, the compiler executes ; immediately. (That is, an
IMMEDIATE word is always executed, even if the system is in compile mode.)What ; does is twofold: first, it installs the code that returns control to
the next outer level of the interpreter; and second, it switches back from
compile mode to interpret mode.
Now try out *+:
DECIMAL 5 6 7 *+ . <cr> 47 ok
This example illustrated two principles of Forth: adding a new word to the dictionary, and trying it out as soon as it was defined.
The diagram below is a flow chart representing the actions performed by the Forth inner interpreter during compilation.
Any word you have added to the dictionary can be decompiled using the Forth
word SEE. Say:
SEE *+ <cr>
and get:
SEE *+
: *+ * + ; ok
This can be useful when trying to understand how something works.
We now discuss the stack and the “reverse Polish” or “postfix” arithmetic based on it. (Anyone who has used a Hewlett-Packard calculator should be familiar with the concept.)
Virtually all modern CPU’s are designed around stacks. Forth efficiently uses its CPU by reflecting this underlying stack architecture in its syntax.
But what is a stack? As the name implies, a stack is the machine analog of a pile of cards with numbers written on them. Numbers are always added to the top of the pile, and removed from the top of the pile. The Forth input line:
2 5 73 -16 <cr> ok
leaves the stack in the state:
cell # contents
0 -16 (TOS)
1 73 (NOS)
2 5
3 2
where TOS stands for “top-of-stack”, NOS for “next-on-stack”, etc.
We usually employ zero-based relative numbering in Forth data structures (such as stacks, arrays, tables, etc.) so TOS is given relative #0, NOS #1, etc.
Suppose we followed the above input line with the line
+ - * . <cr> xxx ok
what would xxx be? The operations would produce the successive stacks
cell# initial + - * .
stack
0 -16 57 -52 -104
1 73 5 2
2 5 2
3 2 empty ( 104 -> CRT )
stack
The operation . (TOS->display) displays -104 to the screen, leaving the stack
empty. That is, xxx is -104.
Forth systems incorporate (at least) two stacks: the parameter stack and the return stack.
A stack-based system must provide ways to put numbers on the stack, to remove them, and to rearrange their order. Forth includes standard words for this purpose.
Putting numbers on the stack is easy: simply type the number (or incorporate it in the definition of a Forth word).
The word DROP removes the number from TOS and moves up all the other numbers.
(Since the stack usually grows downward in memory, DROP merely increments the
pointer to TOS by 1 cell.)
SWAP exchanges the top 2 numbers.
DUP duplicates the TOS into NOS.
ROT rotates the top 3 numbers.
These actions are shown below (we show what each word does to the initial stack):
cell | initial | DROP SWAP ROT DUP
0 | -16 | 73 73 5 -16
1 | 73 | 5 -16 -16 -16
2 | 5 | 2 5 73 73
3 | 2 | 2 2 5
4 | | 2
Forth includes the words OVER, TUCK, PICK and ROLL that act as shown
below (note: PICK and ROLL must be preceded by an integer that says where
on the stack an element gets PICK‘ed or ROLL‘ed):
cell | initial | OVER TUCK 3 PICK 3 ROLL
0 | -16 | 73 -16 2 2
1 | 73 | -16 73 -16 -16
2 | 5 | 73 -16 73 73
3 | 2 | 5 5 5 5
4 | | 2 2 2
Clearly, 0 PICK is the same as DUP, 1 PICK is a synonym for OVER, 1
ROLL means SWAP and 2 ROLL means ROT.
The words PICK and ROLL are mainly useful for dealing with deep stacks. But
the current trend in Forth programming is to avoid making the stack deeper than
3 or 4 elements. A deeper stack than that is generally considered a sign that
the program has been insufficiently thought out and needs to be
factored.
Factoring is the process of breaking out repeated pieces of code from subroutines and giving them a name. This not only shortens the overall program but can make the code simpler. Here is a frequently offereded illustration:
: SUM-OF-SQUARES ( a b -- a*a+b*b ) DUP * SWAP DUP * + ;
has the repeated phrase DUP * and can be replaced profitably by:
: SQUARED ( a -- a*a ) DUP * ;
: SUM-OF-SQUARES ( a b -- a*a+b*b )
SQUARED ( -- a b*b)
SWAP ( -- b*b a)
SQUARED ( -- b*b a*a)
+ ( -- b*b + a*a)
;
The new version of SUM-OF-SQUARES is 2 words shorter and thus easier to read.
Before leaving this subject I would like to offer some deeper examples of
factoring, plus a badly factored definition. To begin with the badly factored
word, look at the file float.f in the Win32Forth main directory, and in
particular at the word >float. This word is almost 3 pages long, which makes
it virtually impossible to read or to maintain.
Here is an example of where factoring leads to great simplification. My linear equations solver uses Gaussian elimination with row-pivoting. By appropriate transformations the equations are put in the form of equations with an upper-triangular matrix. Once this is done the equations can be solved for xk beginning with the n‘th (which only requires a single division to determine the unknown xn); the n-1’st can then be solved by equally simple algebra in terms of xn, etc. This procedure is called “back-solving” because it proceeds in reverse order. The word that does the all the work expects addresses of matrix and inhomogeneous term on the data stack:
: }}solve ( A{{ V{ --)
initialize triangularize back-solve report ;
You will note that the words initialize, triangularize, back-solve and
report were given names that tell you precisely what they do. They represent
the major steps of the algorithm as described above. Of course they have to be
defined before they can be invoked. This is why we describe the typical Forth
programming style as “bottom-up” rather than “top-down” as with other
languages.
My final example of factoring is a routine for adaptive numerical quadrature (integrating a function of one variable) based on Simpson’s Rule. To use it one says:
use( fn.name xa xb err )integral
The algorithm computes the integral on an interval, then breaks it into two equal sub-intervals. The sub-integrals are compared with the original—if they agree within the tolerance the result is accumulated and the integral is evaluated on the remainder of the interval. If they don’t agree the routine works on the upper sub-interval until convergence is achieved.
: )integral ( f: xa xb err -- I[xa,xb]) ( xt --)
initialize
BEGIN \ begin indefinite loop
subdivide \ break last subinterval in two
converged?
IF interpolate \ apply Richardson interpolation
shrink-interval
THEN
none-left UNTIL \ loop until done
TotIntegral F@ ( f: -- Integral) \ leave result
;
This version has been reduced to seven basic operations, not counting the
system words BEGIN, UNTIL that set up the loop; IF…THEN that sets up
the branch, and F@ that puts the answer on the stack.
We have remarked above that compilation establishes links from the calling word to the previously-defined word being invoked. The linkage mechanism—during execution—uses the return stack (rstack): the address of the next word to be invoked is placed on the rstack, so that when the current word is done executing, the system knows to jump to the next word. (This is so in most, but not all, modern Forth implementations. But all have a return stack, whether or not they use them for linking subroutines.)
In addition to serving as a reservoir of return addresses (since words can be
nested, the return addresses need a stack to be put on) the rstack is where the
limits of a DO…LOOP construct are placed.
The user can also store/retrieve to/from the rstack. This is an example of using a component for a purpose other than the one it was designed for. Such use is discouraged for novices since it adds the spice of danger to programming. See “Note of caution” below.
To store to the rstack we say >R, and to retrieve we say R>. The word R@
copies the top of the rstack to the TOS.
Why use the rstack when we have a perfectly good parameter stack to play with? Sometimes it becomes hard to read code that performs complex gymnastics on the stack. The rstack can reduce the complexity.
Alternatively, VARIABLEs—named locations—provide a place to store
numbers—such as intermediate results in a calculation—off the stack, again
reducing the gymnastics. Try this:
\ YOU DO THIS \ EXPLANATION
VARIABLE X <cr> ok \ create a named storage location X;
\ X executes by leaving its address
3 X ! <cr> ok \ ! ("store") expects a number and
\ an address, and stores the number to
\ that address
X @ . <cr> 3 ok \ @ ("fetch") expects an address, and
\ places its contents in TOS.
However, Forth encourages using as few named variables as possible. The reason:
since VARIABLEs are typically global—any subroutine can access them—they can
cause unwanted interactions among parts of a large program.
Although Forth can make variables local to the subroutines that use them (see “headerless words” in FTR), the rstack can often replace local variables:
A note of caution: since the rstack is critical to execution we mess with
it at our peril. If we use the rstack for temporary storage we must restore it
to its initial state. A word that places a number on the rstack must remove
it—using R> or RDROP (if it has been defined)—before exiting that word.
Since DO…LOOP also uses the rstack, for each >R following DO there
must be a corresponding R> or RDROP preceding LOOP. Neglecting these
precautions will probably crash the system.
RDROP is not an ANS Forth word that can be assumed predefined on any system.
Since it is not Standard, some systems call it R>DROP (which also is not
Standard). Here is its definition if needed:
: RDROP ( or R>DROP) ( r: n -- ) R> DROP ;
I mentioned VARIABLEs above—a VARIABLE is a subroutine whose action is to
return the address of a named, cell-sized memory location, as in:
VARIABLE x
x . 247496 ok ( it doesn't have to be this address!)
-49 x !
x @ . -49 ok
A VALUE is a widely used hybrid of VARIABLE and CONSTANT (see below). We
define and initialize a VALUE as we would a CONSTANT:
13 VALUE thirteen ok
We invoke the new VALUE just as we would a CONSTANT:
thirteen . 13 ok
However, we can change a VALUE as though it were a VARIABLE:
47 TO thirteen ok
thirteen . 47 ok
Needless to say, the word TO also works within word definitions, replacing
the VALUE that follows it with whatever is currently in TOS. (Note that it
would be dangerous to follow TO with anything but a VALUE!!) VALUEs are
part of the ANS Forth CORE EXTENSION wordset (that is, the corresponding code
is not guaranteed to be loaded on minimal ANS-compliant systems).
This is a good time to mention that Forth does no type-checking (unless you add
it yourself). You must check that TO is followed by a VALUE and not
something else.
ANS Forth also includes a LOCALS EXTENSION wordset that implements named
memory locations local to a word definition. Locals are generally dynamic in
nature (that is, their memory is reclaimed upon exiting the word), although the
Standard does not insist on this. A commonly used syntax is LOCALS| a b c ...
|, as in this definition (from a line-drawing algorithm):
: v+ ( a b c d -- a+c b+d)
LOCALS| d c b a |
a c + b d + ;
2 3 4 5 v+ .S [2] 6 8 ok.. ( .S displays the stack without destroying it)
The important things to remember are:
the names a, b, c ... can be any Forth-acceptable strings;
the local names have meaning only within a word definition;
the locals are initialized from the stack as shown in v+ above, and as in
the next example:
: test-locals ( a b c -- )
LOCALS| c b a |
CR ." Normal order: " a . b . c .
CR ." Stack order: " c . b . a .
13 TO a 14 TO b 15 TO c \ how TO works
CR ." Changed: " a . b . c
; ok
3 4 5 test-locals
Normal order: 3 4 5
Stack order: 5 4 3
Changed: 13 14 15 ok
the locals act like VALUEs, not like VARIABLEs, as the above example
makes clear;
the LOCALS EXTENSION wordset requires LOCALS| ... | to accomodate (at
least) 8 local names.
LOCALS| ... | is never necessary, nor does it necessarily shorten code, as
the example below makes clear (7 words as opposed to 6 + preamble):
: v+ ( a b c d -- a+c b+d) 2>R R> + SWAP R> + SWAP ;
What it does accomplish is to reduce stack juggling and clarify the code in some cases.
As we just saw, ordinary numbers are fetched from memory to the stack by @
(“fetch”), and stored by ! (store).
@ expects an address on the stack and replaces that address by its contents
using, e.g., the phrase X @
! expects a number (NOS) and an address (TOS) to store it in, and places the
number in the memory location referred to by the address, consuming both
arguments in the process, as in the phrase 3 X !
Double length numbers can similarly be fetched and stored, by D@ and D!, if
the system has these words.
Positive numbers that represent characters can be placed in character-sized
cells of memory using C@ and C!. This is convenient for operations with
strings of text, for example screen and keyboard I/O.
Of course, one cannot put numbers in memory or retrieve them, for that matter, without a means of allocating memory and of assigning labels to the memory so allocated.
The Forth subroutines CREATE and ALLOT are the basic tools for setting
aside memory and attaching a convenient label to it. As we shall see below,
CREATE makes a new dictionary entry, as in
CREATE X
Here the new entry has the name X, but it could have been “Joe” or anything
else. The new name is a Forth subroutine that will return the address of the
next available space in memory. Thus:
CREATE X ok
X . 247316 ok
HERE . 247316 ok
HERE is a subroutine that returns the address of the next available space—we
note that it is the same as the address of X because no space has been
ALLOTted. We can rectify this by saying
10 CELLS ALLOT ok
and checking with
HERE . 247356 ok
We see that the next available space is now marked as 40 bytes further up in
memory. (Each CELL is therefore 4 bytes or 32 bits on this system.) In other
words, the subroutine ALLOT increases the pointer HERE by the number of
address units you have told it to allot. You could have said
40 ALLOT
instead of
10 CELLS ALLOT
but the latter is more portable because it frees you from having to revise your code if you were to run it on a system with 64-bit or 16-bit cells (both of which are in common use).
By executing the sequence
CREATE X 10 CELLS ALLOT
we have set aside enough room to hold 10 32-bit numbers—for example a table or array—that can be referenced by naming it. If we want to get at the 6th element of the array (the first element has index 0, so the 6th has index 5) we would say
X 5 CELLS +
to compute its address. To see how this works, let us say
137 X 5 CELLS + ! ok
to store an integer into the 6th array location; then
X 5 CELLS + @ . 137 ok
retrieves and displays it.
Using the tools provided by CREATE and ALLOT we can devise any sort of data
structure we like. This is why Forth does not provide a panoply of data
structures, such as are to be found in languages like C, Pascal or Fortran. It
is too easy in Forth to custom tailor any sort of data structure one wishes. In
the section on CREATE…DOES> below you will see that Forth makes it easy
to write subroutines (“constructors”) that create custom data structures—that
can even include code fragments that do useful things. For example, a
CONSTANT is a number you would not want to change during a program’s
execution. So you do not want access to its memory location. How then do you
get the number when you need it? You package the code for @ with the storage
location, so that by naming the CONSTANT you retrieve its contents. Its usage
is
17 CONSTANT seventeen ok
seventeen . 17 ok
Forth lets you compare two numbers on the stack, using relational operators
>, <, =. Thus, e.g., the phrase
2 3 > <cr> ok
leaves 0 (“false”) on the stack, because 2 (NOS) is not greater than 3 (TOS). Conversely, the phrase
2 3 < <cr> ok
leaves -1 (“true”) because 2 is less than 3.
Note: In some Forths “true” is +1 rather than -1.
Relational operators consume both arguments and leave a “flag” to show what happened.
(Many Forths offer unary relational operators 0=, 0> and 0<. These, as
might be guessed, determine whether the TOS contains an integer that is 0,
positive or negative.)
The relational words are used for branching and control. For example,
: TEST 0 = INVERT IF CR ." Not zero!" THEN ;
0 TEST <cr> ok ( no action)
-14 TEST <cr>
Not zero! ok
The TOS is compared with zero, and the INVERT operator (bitwise logical
NOT—this flips “true” and “false”) is applied to the resulting flag. The word
CR issues a carriage return (newline). Finally, if TOS is non-zero, IF
swallows the flag and executes all the words between itself and the terminating
THEN. If TOS is zero, execution jumps to the word following THEN.
The word ELSE is used in the IF…ELSE…THEN statement: a nonzero
value in TOS causes any words between IF and ELSE to be executed, and words
between ELSE and THEN to be skipped. A zero value produces the opposite
behavior. Thus, e.g.
: TRUTH CR 0 = IF ." false" ELSE ." true" THEN ;
1 TRUTH <cr>
true ok
0 TRUTH <cr>
false ok
Since THEN is used to terminate an IF statement rather than in its usual
sense, some Forth writers prefer the name ENDIF.
Forth is sometimes accused of being a “write-only” language, i.e. some complain that Forth is cryptic. This is really a complaint against poor documentation and untelegraphic word names. Unreadability is equally a flaw of poorly written FORTRAN, Pascal, C, etc.
Forth offers programmers who take the trouble tools for producing exceptionally clear code.
The word (—a left parenthesis followed by a space—says “disregard all
following text until the next right parenthesis in the input stream”. Thus we
can intersperse explanatory remarks within colon definitions.
A particular form of parenthesized remark describes the effect of a word on the stack. In the example of a recursive loop (GCD below), stack comments are really all the documentation necessary.
Glossaries generally explain the action of a word with a stack-effect comment. For example,
( adr -- n)
describes the word @ (“fetch”): it says @ expects to find an address (adr)
on the stack, and to leave its contents (n) upon completion. The corresponding
comment for ! would be
( n adr -- ) .
\)The word \ (back-slash followed by space) has recently gained favor as a
method for including longer comments. It simply means “drop everything in the
input stream until the next carriage return”. Instructions to the user,
clarifications or usage examples are most naturally expressed in a block of
text with each line set off by \.
ANS Forth contains interpreted IF…THEN, in the form of [IF]…[THEN].
Although they are generally used for conditional compilation, these words
can be used to create comment blocks. Thus we can say
FALSE [IF] anything you want to say
[THEN]
and the included remarks, code, examples or whatever will be ignored by the compiling mechanism.
By eliminating ungrammatical phrases like CALL or GOSUB, Forth presents the
opportunity—via telegraphic names for words—to make code almost as
self-documenting and transparent as a readable English or German sentence.
Thus, for example, a robot control program could contain a phrase like
2 TIMES LEFT EYE WINK
which is clear (although it sounds like a stage direction for Brunhilde to vamp
Siegfried). It would even be possible without much difficulty to define the
words in the program so that the sequence could be made English-like: WINK
LEFT EYE 2 TIMES.
One key to doing this is to eliminate “noise” words like @, !, >R, etc.
by factoring them out into expressively named—and reuseable—subroutines.
Another is to organize the listing of a subroutine so that it physically resembles what it is supposed to do. Two examples are the jump table defined below, as well as a method for programming finite state automata.
The 1979 or 1983 standards require that a conforming Forth system contain a
certain minimum set of pre-defined words. These consist of arithmetic operators
+ - * / MOD /MOD */ for (usually) 16-bit signed-integer (-32767
to +32767) arithmetic, and equivalents for unsigned (0 to 65535), double-length
and mixed-mode (16- mixed with 32-bit) arithmetic. The list will be found in
the glossary accompanying your system, as well as in SF and FTR.
Try this example of a non-trivial program that uses arithmetic and branching to compute the greatest common divisor of two integers using Euclid’s algorithm:
: TUCK ( a b -- b a b) SWAP OVER ;
: GCD ( a b -- gcd) ?DUP IF TUCK MOD GCD THEN ;
The word ?DUP duplicates TOS if it is not zero, and leaves it alone
otherwise. If the TOS is 0, therefore, GCD consumes it and does nothing else.
However, if TOS is unequal to 0, then GCD TUCKs TOS under NOS (to save it);
then divides NOS by TOS, keeping the remainder (MOD). There are now two
numbers left on the stack, so we again take the GCD of them. That is, GCD
calls itself.
If you try the above code it will fail. A dictionary entry cannot be looked up
and found until the terminating ; has completed it. So in fact we must use
the word RECURSE to achieve self-reference, as in
: TUCK ( a b -- b a b) SWAP OVER ;
: GCD ( a b -- gcd) ?DUP IF TUCK MOD RECURSE THEN ;
Now try:
784 48 GCD . <cr> 16 ok
The ANSI/ISO Forth Standard (adopted in 1994) mandates the minimal set of
arithmetic operators + - * / MOD */ /MOD */MOD and M*. The
standard memory-word size is the cell, which must be at least 16 bits, but in
many modern systems is 32- or even 64 bits wide. Single-length integers in
Win32Forth are 32 bits. The stack on ANS-compliant Forths is always 1 cell
wide.
Forth has several ways to loop, including the implicit method of recursion, illustrated above. Recursion has a bad name as a looping method because in most languages that permit recursion, it imposes unacceptable running time overhead on the program. Worse, recursion can—for reasons beyond the scope of this Introduction to Forth—be an extremely inefficient method of expressing the problem. In Forth, there is virtually no excess overhead in recursive calls because Forth uses the stack directly. So there is no reason not to recurse if that is the best way to program the algorithm. But for those times when recursion simply isn’t enough, here are some more standard methods.
The construct
BEGIN xxx ( -- flag) UNTIL
executes the words represented by xxx, leaving TOS (flag) set to TRUE—at which
point UNTIL terminates the loop—or to FALSE—at which point UNTIL jumps back
to BEGIN. Try:
: COUNTDOWN ( n --)
BEGIN CR DUP . 1 - DUP 0 = UNTIL DROP ;
5 COUNTDOWN
5
4
3
2
1 ok
A variant of BEGIN…UNTIL is
BEGIN xxx ( -- flag) WHILE yyy REPEAT
Here xxx is executed, WHILE tests the flag and if it is FALSE leaves the
loop; if the flag is TRUE, yyy is executed; REPEAT then branches back to
BEGIN.
These forms can be used to set up loops that repeat until some external event (pressing a key at the keyboard, e.g.) sets the flag to exit the loop. They can also used to make endless loops (like the outer interpreter of Forth) by forcing the flag to be FALSE in a definition like
: ENDLESS BEGIN xxx FALSE UNTIL ;
Most Forths allow indexed loops using DO…LOOP (or step +LOOP). These
are permitted only within definitions
: BY-ONES ( n --) 0 TUCK DO CR DUP . 1 + LOOP DROP ;
The words CR DUP . 1 + will be executed n times as the lower limit, 0,
increases in unit steps to n-1.
To step by 2’s, we use the phrase 2 +LOOP to replace LOOP, as with
: BY-TWOS ( n --) 0 TUCK
DO CR DUP . 2 + 2 +LOOP DROP ;
These words can be simplified by accessing the loop index with the word I:
: BY-TWOS ( n --) 0 DO CR I . 2 +LOOP ;
We can even count backwards, as in launching a rocket, as in
: countdown 0 SWAP DO CR I . -1 +LOOP ; ok
10 countdown
10
9
8
7
6
5
4
3
2
1
0 ok
One may also nest loops and access the index of the outer loop from the inner
loop using the word J, as in
: NESTED ( n m --) CR
0 DO DUP ( n n --)
0 DO CR J . I .
LOOP
LOOP
DROP ;
2 3 NESTED
0 0
0 1
1 0
1 1
2 0
2 1 ok
Here is something to beware of: suppose the initial indices for the DO loop
are equal: that is, something like
17 17 DO stuff LOOP
then the loop will be executed 232-1 times! As the ANS Standard document says,
“This is intolerable.” Therefore ANS Forth defines a special word, ?DO, that
will skip the loop if the indices are equal, and execute it if they are not. It
is up to the programmer to make sure that if the initial index exceeds the
final one, as in 0 17 DO, the program counts down, assuming that is what was
intended:
0 17 DO stuff -1 +LOOP
N. Wirth invented the Pascal language in reaction to program flow charts
resembling a plate of spaghetti. Such flow diagrams were often seen in early
languages like FORTRAN and assembler. Wirth intended to eliminate line labels
and direct jumps (GOTOs), thereby forcing control flow to be clear and
direct.
The ideal was subroutines or functions that performed a single task, with
unique entries and exits. Unfortunately, programmers insisted on GOTOs, so
many Pascals and other modern languages now have them. Worse, the ideal of
short subroutines that do one thing only is unreachable in such languages
because the method for calling them and passing arguments imposes a large
overhead. Thus execution speed requires minimizing calls, which in turn means
longer, more complex subroutines that perform several related tasks. Today
structured programming seems to mean little more than writing code with nested
IFs indented by a pretty-printer.
Paradoxically, Forth is the only truly structured language in common use,
although it was not designed with that as its goal. In Forth word definitions
are lists of subroutines. The language contains no GOTOs so it is impossible
to write “spaghetti” code. Forth also encourages structure through short
definitions. The additional running time incurred in breaking a long procedure
into many small ones (this is called “factoring”) is typically rather small in
Forth. Each Forth subroutine (word) has one entry and one exit point, and can
be written to perform a single job.
“Top-down” programming is a doctrine that one should design the entire program from the general to the particular:
The natural programming mode in Forth is “bottom-up” rather than “top- down”—the most general word appears last, whereas the definitions must progress from the primitive to the complex. This leads to a somewhat different approach from more familiar languages:
CREATE…DOES> (the pearl of FORTH)Michael Ham has called the word pair CREATE…DOES>, the “pearl of Forth”.
CREATE is a component of the compiler, whose function is to make a new
dictionary entry with a given name (the next name in the input stream) and
nothing else. DOES> assigns a specific run-time action to a newly CREATEd
word.
CREATE finds its most important use in extending the powerful class of Forth
words called “defining” words. The colon compiler : is such a word, as are
VARIABLE and CONSTANT.
The definition of VARIABLE in high-level Forth is simple
: VARIABLE CREATE 1 CELLS ALLOT ;
We have already seen how VARIABLE is used in a program. An alternative
definition found in some Forths is
: VARIABLE CREATE 0 , ;
—these variables are initialized to 0.
Forth lets us define words initialized to contain specific values: for example,
we might want to define the number 17 to be a word. CREATE and , (“comma”)
can do this:
17 CREATE SEVENTEEN , <cr> ok
Now test it via
SEVENTEEN @ . <cr> 17 ok .
Remarks:
, (“comma”) puts TOS into the next cell of the dictionary and
increments the dictionary pointer by that number of bytes.C, (“see-comma”) exists also—it puts a character into the next
character-length slot of the dictionary and increments the pointer by 1 such
slot. (In the ASCII character representation the slots are 1 byte long;
Unicode characters require 2 bytes.)In the preceding example, we were able to initialize the variable SEVENTEEN
to 17 when we CREATEd it, but we still have to fetch it to the stack via
SEVENTEEN @ whenever we want it. This is not quite what we had in mind. We
would like to find 17 in TOS when SEVENTEEN is named. The word DOES> gives
us the tool to do this.
The function of DOES> is to specify a run-time action for the “child” words
of a defining word. Consider the defining word CONSTANT, defined in
high-level (of course CONSTANT is usually defined in machine code for speed)
Forth by
: CONSTANT CREATE , DOES> @ ;
and used as
53 CONSTANT PRIME <cr> ok
Now test it:
PRIME . <cr> 53 ok .
What is happening here?
CREATE (hidden in CONSTANT) makes an entry named PRIME (the first word
in the input stream following CONSTANT). Then , places the TOS (the
number 53) in the next cell of the dictionary.DOES> (inside CONSTANT) appends the actions of all words between it
and ; (the end of the definition)—in this case, @—to the child word(s)
defined by CONSTANT.Here is an example of the power of defining words and of the distinction between compile-time and run-time behaviors.
Physical problems generally involve quantities that have dimensions, usually expressed as mass (M), length (L) and time (T) or products of powers of these. Sometimes there is more than one system of units in common use to describe the same phenomena.
For example, U.S. or English police reporting accidents might use inches, feet and yards; while Continental police would use centimeters and meters. Rather than write different versions of an accident analysis program it is simpler to write one program and make unit conversions part of the grammar. This is easy in Forth.
The simplest method is to keep all internal lengths in millimeters, say, and convert as follows:
: INCHES 254 10 */ ;
: FEET [ 254 12 * ] LITERAL 10 */ ;
: YARDS [ 254 36 * ] LITERAL 10 */ ;
: CENTIMETERS 10 * ;
: METERS 1000 * ;
Note: This example is based on integer arithmetic. The word */ means
“multiply the third number on the stack by NOS, keeping double precision, and
divide by TOS”. That is, the stack comment for */ is ( a b c -- a*b/c).
The usage would be
10 FEET . <cr> 3048 ok
The word [ switches from compile mode to interpret mode while compiling. (If
the system is interpreting it changes nothing.) The word ] switches from
interpret to compile mode.
Barring some error-checking, the “definition” of the colon compiler : is just
: : CREATE ] DOES> doLIST ;
and that of “;” is just
: ; next [ ; IMMEDIATE
Another use for these switches is to perform arithmetic at compile-time rather than at run-time, both for program clarity and for easy modification, as we did in the first try at dimensioned data (that is, phrases such as
[ 254 12 * ] LITERAL
and
[ 254 36 * ] LITERAL
which allowed us to incorporate in a clear manner the number of tenths of millimeters in a foot or a yard.
The preceding method of dealing with units required unnecessarily many
definitions and generated unnecessary code. A more compact approach uses a
defining word, UNITS:
: D, ( hi lo --) SWAP , , ;
: D@ ( adr -- hi lo) DUP @ SWAP CELL+ @ ;
: UNITS CREATE D, DOES> D@ */ ;
Then we could make the table
254 10 UNITS INCHES
254 12 * 10 UNITS FEET
254 36 * 10 UNITS YARDS
10 1 UNITS CENTIMETERS
1000 1 UNITS METERS
\ Usage:
10 FEET . <cr> 3048 ok
3 METERS . <cr> 3000 ok
\ .......................
\ etc.
This is an improvement, but Forth permits a simple extension that allows conversion back to the input units, for use in output:
VARIABLE <AS> 0 <AS> !
: AS TRUE <AS> ! ;
: ~AS FALSE <AS> ! ;
: UNITS CREATE D, DOES> D@ <AS> @
IF SWAP THEN
*/ ~AS ;
\ UNIT DEFINITIONS REMAIN THE SAME.
\ Usage:
10 FEET . <cr> 3048 ok
3048 AS FEET . <cr> 10 ok
Suppose we have a series of push-buttons numbered 0-3, and a word WHAT to
read them. That is, WHAT waits for input from a keypad: when button #3 is
pushed, for example, WHAT leaves 3 on the stack.
We would like to define a word BUTTON to perform the action of pushing the
n’th button, so we could just say:
WHAT BUTTON
In a conventional language BUTTON would look something like
: BUTTON DUP 0 = IF RING DROP EXIT THEN
DUP 1 = IF OPEN DROP EXIT THEN
DUP 2 = IF LAUGH DROP EXIT THEN
DUP 3 = IF CRY DROP EXIT THEN
ABORT" WRONG BUTTON!" ;
That is, we would have to go through two decisions on the average.
Forth makes possible a much neater algorithm, involving a “jump table”. The
mechanism by which Forth executes a subroutine is to feed its “execution token”
(often an address, but not necessarily) to the word EXECUTE. If we have a
table of execution tokens we need only look up the one corresponding to an
index (offset into the table) fetch it to the stack and say EXECUTE.
One way to code this is
CREATE BUTTONS ' RING , ' OPEN , ' LAUGH , ' CRY ,
: BUTTON ( nth --) 0 MAX 3 MIN
CELLS BUTTONS + @ EXECUTE ;
Note how the phrase 0 MAX 3 MIN protects against an out-of-range index.
Although the Forth philosophy is not to slow the code with unnecessary error
checking (because words are checked as they are defined), when programming a
user interface some form of error handling is vital. It is usually easier to
prevent errors as we just did, than to provide for recovery after they are
made.
How does the action-table method work?
CREATE BUTTONS makes a dictionary entry BUTTONS.' (“tick”) finds the execution token (xt) of the following word,
and the word , (“comma”) stores it in the data field of the new word
BUTTONS. This is repeated until all the subroutines we want to select
among have their xt’s stored in the table.BUTTONS now contains xt’s of the various actions of BUTTON.CELLS then multiplies the index by the appropriate number of bytes per
cell, to get the offset into the table BUTTONS of the desired xt.BUTTONS + then adds the base address of BUTTONS to get the absolute
address where the xt is stored.@ fetches the xt for EXECUTE to execute.EXECUTE then executes the word corresponding to the button pushed. Simple!If a program needs but one action table the preceding method suffices. However, more complex programs may require many such. In that case it may pay to set up a system for defining action tables, including both error-preventing code and the code that executes the proper choice. One way to code this is
: ;CASE ; \ do-nothing word
: CASE:
CREATE HERE -1 >R 0 , \ place for length
BEGIN BL WORD FIND \ get next subroutine
0= IF CR COUNT TYPE ." not found" ABORT THEN
R> 1+ >R
DUP , ['] ;CASE =
UNTIL R> 1- SWAP ! \ store length
DOES> DUP @ ROT ( -- base_adr len n)
MIN 0 MAX \ truncate index
CELLS + CELL+ @ EXECUTE ;
Note the two forms of error checking. At compile-time, CASE: aborts
compilation of the new word if we ask it to point to an undefined subroutine:
case: test1 DUP SWAP X ;case
X not found
and we count how many subroutines are in the table (including the do-nothing
one, ;case) so that we can force the index to lie in the range [0,n].
CASE: TEST * / + - ;CASE ok
15 3 0 TEST . 45 ok
15 3 1 TEST . 5 ok
15 3 2 TEST . 18 ok
15 3 3 TEST . 12 ok
15 3 4 TEST . . 3 15 ok
Just for a change of pace, here is another way to do it:
: jtab: ( Nmax --) \ starts compilation
CREATE \ make a new dictionary entry
1- , \ store Nmax-1 in its body
; \ for bounds clipping
: get_xt ( n base_adr -- xt_addr)
DUP @ ( -- n base_adr Nmax-1)
ROT ( -- base_adr Nmax-1 n)
MIN 0 MAX \ bounds-clip for safety
1+ CELLS+ ( -- xt_addr = base + 1_cell + offset)
;
: | ' , ; \ get an xt and store it in next cell
: ;jtab DOES> ( n base_adr --) \ ends compilation
get_xt @ EXECUTE \ get token and execute it
; \ appends table lookup & execute code
\ Example:
: Snickers ." It's a Snickers Bar!" ; \ stub for test
\ more stubs
5 jtab: CandyMachine
| Snickers
| Payday
| M&Ms
| Hershey
| AlmondJoy
;jtab
3 CandyMachine It's a Hershey Bar! ok
1 CandyMachine It's a Payday! ok
7 CandyMachine It's an Almond Joy! ok
0 CandyMachine It's a Snickers Bar! ok
-1 CandyMachine It's a Snickers Bar! ok
Although Forth at one time eschewed floating point arithmetic (because in the era before math co-processors integer arithmetic was 3x faster), in recent years a standard set of word names has been agreed upon. This permits the exchange of programs that will operate correctly on any computer, as well as the development of a Scientific Subroutine Library in Forth (FSL).
Although the ANS Standard does not require a separate stack for floating point numbers, most programmers who use Forth for numerical analysis employ a separate floating point stack; and most of the routines in the FSL assume such. We shall do so here as well.
The floating point operators have the following names and perform the actions indicated in the accompanying stack comments:
F@ ( adr --) ( f: -- x)
F! ( adr --) ( f: x --)
F+ ( f: x y -- x+y)
F- ( f: x y -- x-y)
F* ( f: x y -- x*y)
F/ ( f: x y -- x/y)
FEXP ( f: x -- e^x)
FLN ( f: x -- ln[x])
FSQRT ( f: x -- x^0.5)
Additional operators, functions, trigonometric functions, etc. can be found in
the FLOATING and FLOATING EXT wordsets. (See dpANS6— available in HTML,
PostScript and MS Word formats. The HTML version can be accessed from this
homepage.)
To aid in using floating point arithmetic I have created a simple FORTRAN-like interface for incorporating formulas into Forth words.
The file ftest.f (included below) illustrates how ftran201.f should be used.
\ Test for ANS FORmula TRANslator
marker -test
fvariable a
fvariable b
fvariable c
fvariable d
fvariable x
fvariable w
: test0 f" b+c" cr fe.
f" b-c" cr fe.
f" (b-c)/(b+c)" cr fe. ;
3.e0 b f!
4.e0 c f!
see test0
test0
: test1 f" a=b*c-3.17e-5/tanh(w)+abs(x)" a f@ cr fe. ;
1.e-3 w f!
-2.5e0 x f!
cr cr
see test1
test1
cr cr
: test2 f" c^3.75" cr fe.
f" b^4" cr fe. ;
see test2
test2
\ Baden's test case
: quadroot c f! b f! a f!
f" d = sqrt(b^2-4*a*c) "
f" (-b+d)/(2*a) " f" (-b-d)/(2*a) "
;
cr cr
see quadroot
: goldenratio f" max(quad root(1,-1,-1)) " ;
cr cr
see goldenratio
cr cr
goldenratio f.
0 [IF]
Output should look like:
: test0
c f@ b f@ f+ cr fe. c f@ fnegate b f@ f+ cr fe. c f@ fnegate b f@
f+ c f@ b f@ f+ f/ cr fe. ;
7.00000000000000E0
-1.00000000000000E0
-142.857142857143E-3
: test1
x f@ fabs 3.17000000000000E-5 w f@ ftanh f/ fnegate b f@ c f@ f* f+
f+ a f! a f@ cr fe. ;
14.4682999894333E0 ok
: test2
c f@ noop 3.75000000000000E0 f** cr fe. b f@ f^4 cr fe. ;
181.019335983756E0
81.0000000000000E0 ok
: QUADROOT C F! B F! A F! B F@ F^2 flit 4.00000 A F@
C F@ F* F* F- FSQRT D F! B F@ FNEGATE D
F@ F+ flit 2.00000 A F@ F* F/ B F@ FNEGATE
D F@ F- flit 2.00000 A F@ F* F/ ;
: GOLDENRATIO flit 1.00000 flit -1.00000 flit -1.00000
QUADROOT FMAX ;
1.61803 ok
with more or fewer places.
[THEN]
To illustrate how to construct a non-trivial program, let us develop a binary
search root-finder. We will use the FORmula TRANslator ftran201.f to simplify
the appearance of the code (that is, it hides the data fetches and stores that
would otherwise be required).
First we need to understand the algorithm thoroughly:
If we know that the roots are bracketed between xa and xb, and that
f(xa)*f(xb) < 0 (at least 1 root lies in the interval) we take the next guess
to be xp = (xa+xb)/2.
We then evaluate the function at xp: fp = f(xp). If fa*fp > 0 we set xa
= xp, else we set xb = xp. We repeat until the ends of the interval
containing the root are sufficiently close together.
To begin programming, we note that we will have to keep track of three points:
xa, xb and xp. We also have to keep track of three function values
evaluated at those points, Ra, Rb and Rp. We also need to specify a
precision, epsilon, within which we expect to determine the root.
Next we need to define the user interface. That is, once we have a subroutine that finds roots, how will we invoke it? Since we would like to be able to specify the name of the function to find the root of at the same time we specify the interval we think the root is in, we need some way to pass the name to the root finder as an argument.
I have previously developed an interface that suits me: I say
use( fn.name xa xb precision )bin_root
as in
use( f1 0e0 2e0 1e-5 )bin_root
and the root will be left on the floating point stack.
The code for passing names of functions as arguments is included when you load
ftran201.f—the words used in this program are use(, v: and defines.
v: creates a dummy dictionary entry (named dummy in the program) which can
be made to execute the actual function whose name is passed to the word
)bin_root.
Here are the data structures and their identifications:
MARKER -binroots \ say -binroots to unload
\ Data structures
FVARIABLE Ra \ f(xa)
FVARIABLE Rb \ f(xb)
FVARIABLE Rp \ f(xp)
FVARIABLE xa \ lower end
FVARIABLE xb \ upper end
FVARIABLE xp \ new guess
FVARIABLE epsilon \ precision
v: dummy \ create dummy dictionary entry
The actual root-finding subroutine, )bin_root, will be quite simple and easy
to follow:
: )bin_root ( xt --) ( f: Low High Precision -- root)
initialize
BEGIN NotConverged? WHILE NewPoint REPEAT
f" (xa+xb)/2" ( f: -- root)
;
Note that the subroutines comprising it are telegraphically named so they need
no explanation; whereas )bin_root itself is explained by its stack comments.
The comments on the first line indicate that )bin_root expects an “execution
token” on the data stack, and three floating point numbers on the floating
point stack. These are its arguments. (See 11d for a discussion of EXECUTE,
etc.) The execution token is what is used to change the behavior of the dummy
dictionary entry dummy : we say
defines dummy
in the word initialize to make dummy behave like the function whose root we
are seeking.
The final comment ( f: -- root) indicates that )bin_root leaves the answer
on the floating point stack.
In a sense we are programming from the top down, since we have begun with the last definition of the program and are working our way forward. In Forth we often go both ways—top-down and bottom-up—at the same time.
The key words we must now define are initialize, NotConverged? and
NewPoint. We might as well begin with initialize since it is conceptually
simple:
: initialize ( xt --) ( f: lower upper precision --)
defines dummy \ xt -> DUMMY
f" epsilon=" f" xb=" f" xa=" \ store parameters
f" Ra=dummy(xa)"
f" Rb=dummy(xb)"
f" MoreThan( Ra*Rb, 0)" \ same sign?
ABORT" Even # of roots in interval!"
;
The word ABORT" prints the message that follows it and aborts execution, if
it encounters a TRUE flag on the data stack. It is widely used as a simple
error handler. ABORT (without the ") simply aborts execution when it is
encountered. So it usually is found inside some decision structure like an
IF…THEN clause. (See 11d for two examples of usage.)
ABORT" was preceded by a test. In order to use a test as a function in a
Fortran-like expression (this test consumes two arguments from the floating
point stack and leaves a flag on the data stack), we must define a synonym for
it. The reason is that ftran201.f does not recognize relational operators
like > or <. The definition is1:
: MoreThan ( f: a b) ( -- true if a>b)
POSTPONE F> ; IMMEDIATE
The code produced by f" MoreThan( Ra*Rb, 0)" is then just
RA F@ RB F@ F* flit 0.00000E-1 F>
which is what we want. We have already explained the phrase defines dummy. The
phrases f" xa=" and so on are shorthand for storing something from the
floating point stack to a floating point variable. Thus f" xa=" generates the
code XA F!. The rest of initialize is to calculate the function at the
endpoints of the supposed bounding interval (a,b).
NotConverged? is a test for (non)convergence. WHILE expects a flag on the
data stack, as described in 10a. So we define
: NotConverged? ( -- f)
f" MoreThan( ABS( xa - xb ), epsilon )" ;
which generates the code
XB F@ XA F@ F- FABS EPSILON F@ F>
What about NewPoint? Clearly,
: NewPoint
f" xp = (xa+xb)/2" \ new point
f" Rp = dummy(xp)"
f" MoreThan( Ra*Rp, 0)" \ xp on same side of root as xa?
IF f" xa=xp" f" Ra=Rp"
ELSE f" xb=xp" f" Rb=Rp" THEN
;
That is, we generate a new guess by bisection, evaluate the function there and decide how to choose the new bounding interval.
All that remains is to put the definitions in the proper order and test the
result by loading the program bin_rts.f and trying out the test case.
FALSE [IF]
Usage example:
: f1 fdup fexp f* 1e0 f- ; ok
use( f1 0e0 2e0 1e-5 )bin_root f. .567142 ok
[THEN]
Finally, if we want to be very careful indeed, and/or are planning to re-use
the program, we add an appropriate boilerplate header, such as that included in
the file bin_rts.f.
As in other languages, alphanumeric strings in Forth are represented as contiguous arrays in memory, each memory unit being a “character”. Traditionally a character encoded by the ASCII or EBCDIC systems occupied one (1) byte of storage, allowing for 256 characters. With the need to encode alphabets other than the Latin one (e.g. Chinese, Arabic, Hebrew, Cyrillic) a two-byte encoding called Unicode has been adopted, which allows for 65535 distinct characters.
A traditional Forth string consisted of a count byte and up to 255 bytes containing alphanumeric characters (usually in ASCII). In ANS Forth this scheme has been abandoned: how strings are stored will depend on the implementation. However ANS Forth contains words that enable us to manipulate strings without reference to how they are implemented.
Most ANS Forths (and Win32Forth is one of them) define S" to have defined
interpretive as well as compiling behavior. This means that if we say
S" This is a string!" CR TYPE
we get
This is a string! ok
What happened? S" This is a string!" created a string with text beginning at
a “c-address” and with a “count” that says how many characters (including
blanks) the string includes. The address and count are left on the stack. That
is, the proper stack picture would be
S" This is a string!" ( -- c-addr u)
(the count is an unsigned integer u because strings of negative length are meaningless).
The word CR means “insert a carriage return”, and TYPE means “from the
c-addr output u characters to the screen”.
Exercise:
Use what you have just learned to write a “Hello world!” program.
It is perfectly feasible to define one’s own word set for working with strings, depending on what sort of application one is writing. For example, I have written a program to translate mathematical formulas in Fortran-like form into Forth code, outputting the result either to the screen (for test purposes) or embedding it into a Forth definition. There is even a variant that evaluates the formula, provided all the variables have been previously defined and given numerical values. To accomplish this required strings longer than 255 characters, so I defined my own.
I now want to turn to “pictured numerical output”. Many computer programs need to output numbers in some particular format, no matter how they are stored intern- ally. For example an accounting program might output monetary amounts in the usual dollars-and-cents format. The Forth words that accomplish this are
# , <# , #S , #> , SIGN and HOLD
They do not have any defined interpretive behavior (although there is no telling what any particular Forth may do) and are intended to be used within word definitions. Here is an example: suppose we are writing an accounting program. Since most users will not be dealing with amounts that exceed $100,000,000 we can use signed 32-bit integers to represent the dollars and cents. (Such numbers can represent amounts up to ±(231—1) = ±2147483647 cents.) Signed double-length integers are at least 32 bits long on all ANS-compatible systems (although they will be 64 bits on 32-bit computers). Hence we shall use doubles so the program will run on any ANS-compatible Forth.
A double-length integer is entered from the keyboard by including a decimal point in it, as
-4756.325 ok
Let us define a word to output a double-length integer. The first part will be to translate it to an alphanumeric string referred to by c-addr u.
: (d.$) ( d -- c-adr u) TUCK DABS <# # # [CHAR] . HOLD #S ROT SIGN #> ;
As the stack comment ( d -- c-adr u) shows, (d.$) consumes a (signed)
double-length integer from the stack and leaves the string data in a form that
can be printed to the screen by the word TYPE. Let us test this:
4376.58 (d.$) CR TYPE
4376.58 ok
-4376.99 (d.$) CR TYPE
-4376.99 ok
It is worth exploring what each part does. A double length integer is stored as
two cells on the stack, with the most-significant part on TOS. Thus the word
TUCK places the most-significant part (containing the algebraic sign) above d
and then DABS converts d to |d|. Next, <# begins the process of
constructing an alphanumeric string. The two instances of # peel off the two
least-significant digits and put them in the string. The phrase [CHAR] .
HOLD adds a decimal point to the string.
[CHAR] builds in the representation of the character . as a numeric literal
(in ASCII it is 46). HOLD then adds it to the string under construction.
(HOLD has no meaning except between <# and #>.) Then the word #S takes
the rest of the digits and adds them to the nascent string.
(Semi)finally, ROT puts the most significant part of d (with its sign) on
TOS, and SIGN adds its algebraic sign to the beginning of the string. (Again,
SIGN is only meaningful between <# and #>.)
And finally, the word #> cleans everything up and leaves c-addr u on the
stack, ready for display or whatever.
Exercises:
Most Forths include an assembler that makes programming in machine code almost as easy as programming in high level Forth. Why would one want to do that? There are reallly only two reasons for dropping into machine language:
In this section we deal only with the second reason. We imagine that after careful algorithmic analysis there is no way to further speed up a high level program. However the requirements of the application demand a substantial speed improvement. Since most Forths are somewhat inefficient relative to optimized C or Fortran, there may be a substantial speed gain to be realized from hand-coding in assembly language. An example is the innermost loop in a linear equations solver. For n equations it is executed n3 times. Moreover it is a very simple loop, containing 2 fetches, a multiplication, a subtraction and a store. Thus it is a perfect candidate to be optimized. By contrast, the middle- and outermost loops are executed respectively n2 and n times, so there is little point in optimizing them (that is, for small matrices the running time is too short to care; whereas for large matrices—n > 100—the middle loop would have to run 100× faster to be worth rewriting in machine code.
It is important to realize that assembly language conventions differ from Forth to Forth. Moreover the instruction set will be particular to a given target computer. That is, there is no such thing as a generic assembler in any programming environment, much less for Forth. Hence everything we do here will be specific to Win32Forth running on a Pentium-class machine.
We begin with a little warmup exercise. Suppose I found that my program used
the sequence * + many times. Obviously good factoring practice would dictate
that this sequence be given its own name and defined as a new subroutine
(word). So we might define
: *+ * + ;
and substitute it for the sequence * + throughout the program. But suppose
we discover that this short sequence is the bottleneck in our program’s running
time, so that speeding it up will greatly increase speed of execution. (I
realize it isn’t likely for this example—bear with me!) So we would like to
translate it into machine code. To do this we first look at the machine code
for * and + separately. These are primitive words and almost certainly will
be CODE definitions in any reasonable Forth.
Thus we need to disassemble these words. In some Forths this might mean
inspecting the contents of the word byte by byte, and looking up the code
sequences in the operating manual for that CPU. Fortunately for us, Win32Forth
has a built-in disassembler. If we SEE a CODEd definition it will return
the actual byte-codes as well as the names of the instructions in the
Win32Forth assembler. Let us try this out: we get
see +
+ IS CODE
4017AC 58 pop eax
4017AD 03D8 add ebx, eax
ok
see *
* IS CODE
401B9C 8BCA mov ecx, edx
401B9E 58 pop eax
401B9F F7E3 mul ebx
401BA1 8BD8 mov ebx, eax
401BA3 8BD1 mov edx, ecx
ok
To understand these sequences we must bear in mind that Win32Forth keeps TOS in
a 32-bit register, in fact the ebx register. We must also know that
Win32Forth uses the edx register for something or other—probably to do with the
mechanism for executing a word and returning control to the next word in the
program (that is, the threading mechanism). So if a program is going to modify
the edx register, its previous contents have to be saved somewhere. Since
addition of eax to ebx does not affect edx, the CODE for + doesn’t
need to protect edx; however, when two 32-bit numbers are multiplied, the
result can contain as many as 64 bits. Thus the product occupies the two
registers eax (bits 0 through 31) and edx (bits 32-63).
This is the reason for saving edx into the unused ecx register, and then
restoring it afterward.
It is worth noting, before we go too far, that the Win32Forth assembler preserves the Intel conventions. That is,
add ebx, eax
adds the contents of register eax to ebx, leaving the result in ebx
(which is where we want it because that is TOS). Similarly, the sequences
mov ecx, edx
and
mov ebx, eax
have the structure
mov destination, source
We should also ask why the integer multiplication instruction
mul ebx
has only one operand. The answer is that the register eax is the so-called
“accumulator”, so it contains one of the multiplicands initially and then it
and edx contain the product, as noted above. It is then only necessary to
specify where the other multiplicand is coming from (it could be a cell in
memory).
Therefore to define the word *+ in assembler we would type in
CODE *+ ( a b c -- b*c+a) \ stack: before -- after
mov ecx, edx \ protect edx because mul alters it
pop eax \ get item b; item c (TOS) is already in ebx
mul ebx \ integer multiply-- c*b -> eax (accumulator)
pop ebx \ get item a
add ebx, eax \ add c*b to a -- result in ebx (TOS) --done
mov edx, ecx \ restore edx
next, \ terminating code for Forth interpreter
END-CODE ok
Note that the Forth assembler recognizes Forth comments—Intel-style comments would be preceded by semicolons, but we obviously can’t use these because semicolon is a Forth word.
The word END-CODE has an obvious meaning, but what about next, (the comma
is part of the name and is significant!). Advanced users of the assembler
sometimes need to define code sequences that do not include the instructions to
transfer control to the next word. So Win32Forth has factored this function out
of the CODE terminating sequence. For this example we require these
instructions to be assembled, so we include next,.
Before going further, you should try out this example and convince yourself it works.
For our nontrivial example we are going to hand-code the innermost loop of my linear equations solver. I programmed this in high-level Forth in the form
: }}r1-r2*x ( M{{ r1 r2 -- ) ( f: x -- x) \ initialize assumed
0 0
LOCALS| I1 I2 r2 r1 mat{{ | \ local names
frame| aa | \ local fvariable
Iperm{ r1 } @ TO I1
Iperm{ r2 } @ TO I2
Nmax r2 ?DO \ begin loop
f" mat{{ I1 I }} = mat{{ I1 I }}
- mat{{ I2 I }} * aa"
LOOP \ end loop
f" aa" |frame ( f: -- x)
;
Here Iperm{ is the name of an array of integers that holds the permuted
row-labels; note that the rows we work on do not change within the actual loop.
Neither does the floating point number represented by the local variable aa.
What does change are the row-elements.
To translate }}r1-r2*x to assembler we will need to factor it a bit more
finely. Evidently we are subtracting the I‘th element of row I2, multiplied
by aa, from the I‘th element of row I1. Moreover, since the matrix has
been partially triangularized already, we do not start with element 0 but with
element r2. Finally, as we have noted previously, ?DO includes a bounds
check so that if r2 equals or is greater than Nmax the loop is not
executed. So we shall revise }}r1-r2*x to include this test explicitly and
CODE only the loop itself. That is, we shall write
: incr_addrs ( addr1 addr2 -- addr1+inc addr2+inc)
[ 1 FLOATS ] LITERAL
TUCK + -ROT + SWAP ;
: inner_loop ( addr1 addr2 Nmax lower_limit -- ) ( f: x -- x)
DO \ begin loop
( f: aa) ( addr1 addr2) \ loop invariant
2DUP SWAP F@ ( f: aa m[I1,I])
FOVER F@ F* F- OVER F!
\ m[I1,I = m[I1,I] - m[I2,I]*x
( f: x) ( addr1 addr2) \ loop invariant
incr_addrs \ increment addresses
LOOP \ end loop
2DROP
;
: }}r1-r2*x ( M{{ r1 r2 -- ) ( f: x -- x) \ initialize assumed
0 0
LOCALS| I1 I2 r2 r1 mat{{ | \ local names
Iperm{ r1 } @ TO I1
Iperm{ r2 } @ TO I2
Nmax r2 >
IF mat{{ I1 r2 }} mat{{ I1 r2 }} \ base adresses
Nmax r2 \ loop limits
( f: x) ( addr1 addr2 Nmax lower_limit)
inner_loop
( f: x) ( -- )
THEN
;
So what we are going to CODE here is the word inner_loop, since these are
the only instructions executed n3 times.
CODE inner_loop ( addr1 addr2 Nmax lower_limit -- ) ( f: x -- x)
fld FSIZE FSTACK_MEMORY \ f: -> fpu:
mov ecx, ebx \ ecx = r2
pop eax \ eax = Nmax
( addr1 ebx=addr2)
push edx ( addr1 edx ebx)
mov edx, 4 [esp] \ edx = addr1)
\ begin loop
L$1: fld [ebx] [edi] ( fpu: aa m[addr2]
fmul st, st(1) ( fpu: aa m2*aa)
fld [edx] [edi] ( fpu: aa m2*aa m1)
fxch st(1) ( fpu: aa m1 m2*aa)
fsubp st(1), st ( fpu: aa m1-m2*aa)
fstp [edx] [edi] ( fpu: aa)
add [edx], # 8 \ increment addresses
add [ebx], # 8
inc ecx \ add 1 to loop variable
cmp eax, ecx \ test for done
jl L$1 \ loop if I < Nmax
\ end loop
pop edx \ restore edx
pop ebx
pop ebx \ clean up data stack
fstp FSIZE FSTACK_MEMORY \ fpu: -> f:
next,
END-CODE
A final remark: I have written a tool for translating automatically a sequence
of floating point operations to CODE for the Intel FPU. This tool, ctran.f,
is specialized for Win32Forth.
the word POSTPONE in this context means that the word following it—in this
case F>—will be compiled into the word that uses MoreThan rather than in
MoreThan itelf. (Note that MoreThan is IMMEDIATE.) This way of doing
things saves some overhead during execution. Some Forths (notably Win32Forth)
define a word SYNONYM to accomplish the same thing. ↩